Modeling Kerr non-linear devices

Main Researcher: Bjorn Maes

Non-linear materials are actively researched for designing all-optical devices. The Kerr effect is a promising nonlinearity as it means a near-instantaneous intensity dependent refractive index change. Because of the weakness of this effect strong field confinements are necessary, which are now possible in advanced structures such as photonic crystals or photonic wires. To simulate these devices efficient and accurate new methods are needed.
We developed an extension to the linear mode expansion method. In this way we inherit many of the benefits of the original method, such as advanced boundary conditions, rigorousness, small computational domain, etc.
Our method consists of an iteration of linear calculations, using CAMFR. The non-linear material is divided in a grid and each small rectangle is assigned its refractive index during iteration.

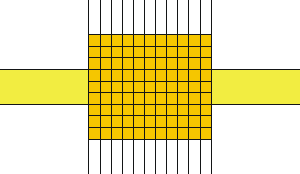
Example of a spatial grid.

Starting from the linear index distribution, a guess or a previously calculated solution, we perform a linear eigenmode simulation. This gives us the intensities in the rectangles with which we can update the indexes using the Kerr constitutive relation of the material. If the new index distribution is approximately equal to the old one, we have converged to a solution of the full non-linear problem.
We have implemented this algorithm for finite and periodic infinite structures. Calculations are especially fast for structures with small non-linear sections, as the linear parts only have to be simulated once.

A nonlinear photonic crystal switch (Soljacic et al, 2002).

As mode expansion is a frequency domain technique we immediately obtain steady-state solutions. For this purpose time domain methods such as Finite-Difference Time-Domain (FDTD) require the simulation of long pulses.
We employ modes propagating in both directions, thus reflection and interference effects can be observed. This feedback in combination with nonlinearity can give rise to bistability, which means two possible outputs for one input. Our algorithm is able to track both branches of such bistable solution curves. FDTD needs a strong input excitation pulse before the main pulse to scan the upper branch, which complicates matters.

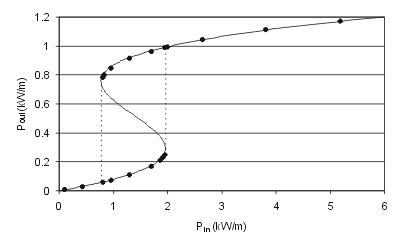
Bistable solution of the photonic crystal switch.

Other people involved:

• Abdoulghafar Omari
• Bjorn Maes

PhD thesises